Stats with Cats: 21 Terms Experimenters Need to Know
Statistics are the underpinning of our experiment results—they help us make an educated decision on a test result with incomplete data. In order to run statistically sound A/B tests, it’s essential to invest in an understanding of these key concepts. Use this index of terms as a primer for future reading on statistics, and keep this glossary handy for your next deep dive into experiment results with your team. No prior knowledge of statistics needed.

Shana Rusonis

 “Um, when are we going to use this, again?”
“Um, when are we going to use this, again?”
The classroom woes of teenagers everywhere have returned to haunt us—the concepts many of us left behind in high-school math textbooks are now highly relevant to the success of our A/B testing strategies.
For most of us, it’s been years since we last thought about a chi-square test or calculated a p-value. It’s time to dig in again.
Why? Statistics are the underpinning of our experiment results—they help us make an educated decision on a test result with incomplete data. In order to run statistically sound A/B tests, it’s essential to invest in an understanding of these key concepts.

Go in depth with stats for experiments with this eBook.
Use this index of terms as a primer for future reading on statistics, and keep this glossary handy for your next deep dive into experiment results with your team. No prior knowledge of statistics is required to understand these terms; however, some of the concepts are interrelated, so you may find yourself jumping between definitions as you read.
If you want to explore the terms in more detail (or are allergic to cats), download the Practical Guide to Statistics for Online Experiments.
21 Statistical Terms Experimenters Need to Know
- Bayesian Statistics: A statistical method that takes a bottom-up approach to data analysis when calculating statistical significance. This means that past knowledge of similar experiments is encoded into a statistical device known as a prior, and this prior is combined with current experiment data to make a conclusion on currently running experiment.
- Confidence Interval: A computed range used to describe the certainty of an estimate of some underlying parameter. In the case of A/B testing, these underlying parameters are conversion rates, or improvement rates. Confidence intervals have a few theoretical interpretations, most practically an interval with a certain probability of containing the true improvement (e.g., 95% probability of containing the true improvement.)

– A winning variation will have a confidence interval entirely above 0 – An inconclusive variation will have a confidence interval that includes 0 – A losing variation will have a confidence interval entirely below 0
- Continuous Monitoring: The behavior of repeatedly checking experiment results. This is an unsafe method of conducting an experiment with traditional statistics, since it is tempting to stop an experiment when it reaches statistical significance the first time, even if it is before the needed sample size for that effect.
- Effect Size: The amount of difference between the original and variant of a test. This is an input in many sample size calculators used for fixed horizon testing (the “MDE”.) In Optimizely, this is “Improvement.”
- Error Rate: The chance of finding a conclusive difference between a control and variation in an A/B test by chance alone OR not finding a difference when there is one. This encompasses both type I and type II errors, or false positives and false negatives, respectively.
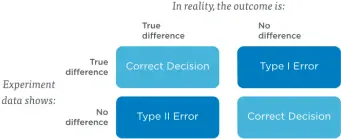
A false positive is an experiment result that shows a difference when none actually exists. A false negative is an experiment result that shows no difference when one actually exists.
- False Positive Rate: The odds of encountering a type I error, or finding a significant result when none actually exists. It can be computed by dividing the number of false positives by (total number of false positives + true negatives.)
- False Discovery Rate: The odds of encountering type I errors in experiments with many simultaneous goal and variation combinations, which can be inflated above what is typically expected at a given significance threshold. The expected number of false discoveries—incorrect winners and losers—computed by dividing the number of false positives by the total number of significant results.
Learn more about False Discovery Rate >>
- Fixed Horizon Hypothesis Test: A hypothesis test that makes use of traditional statistical methods—typically, these statistical methods are powered by a t-test designed for an experimenter making a decision at a specific moment in time (ideally after reaching preset sample size of experiment visitors.)
- Frequentist Statistics: A statistical method that makes predictions on underlying truths of the experiment using only data from the current experiment when calculating statistical significance. Frequentist arguments are more counter-factual in nature, and resemble the type of logic that lawyers use in court.
- Hypothesis Test: Sometimes called a t-test, a statistical inference methodology used to determine if an experiment result was likely due to chance alone. Hypothesis tests try to disprove a null hypothesis, the assumption that two variations are the same. In the context of A/B testing, Hypothesis tests will help determine the probability that one variation is better than the other, supposing the variations were actually the same.

If our null hypothesis is proved false, we would have some very exciting experiment results on our paws.
- Improvement: Sometimes known as ‘lift’ or ‘effect size,’ A performance change for an experimental treatment (variation) in either the positive or negative direction. This could mean an increase in conversion rate, a positive improvement; or a decrease in conversion rate, a negative improvement.
- Null Hypothesis: The pretense upon which statistical significance is calculated. This is the assumption that the experimental treatment (variation) will perform the same as the original. When statistical significance is calculated, it represents the likelihood of rejecting the null hypothesis, or the likelihood that there is actually a difference between the variation and original. The goal of a hypothesis test is to disprove this null hypothesis that the two variations are the same.
- P-Value: The chance that you discovered a statistically significant difference between a variation and control in your experiment by random chance. When quantified, it answers the question: How likely is it this improvement happened, if the null hypothesis were true and there really is no difference between my variation and control? In other words, how likely is it that the observed conversion rate difference for a test was due to random chance? This can also be thought of as the type 1 error rate of a test.
- Sample Size Calculator: A method for reducing type I error in hypothesis testing under the assumption of a fixed horizon test. Setting a sample size for a test before starting the experiment sets expectations for how long an experiment should collect data before computing the results.

At an MDE of 5%, our experiment will need to run for 5 cat lives before we reach statistically significant results.
- Sequential Hypothesis Test: A subset of hypothesis testing where an experimenter can make a decision about their test at any time. In this case, there is no “horizon” for the test, and continuous monitoring does not introduce the risk of increased false positives (errors) as it would in a fixed horizon hypothesis test.
- Statistical Confidence: The likelihood that a null hypothesis is not true. It can be thought of as the chance or “confidence” that a variation is different than the variation. It is calculated as (1 – p-value) and is “Statistical Significance” in Optimizely’s results page.
- Statistical Error: A statistical error is a result that reaches statistical significance that does not represent a significant result. Statistical errors happen because of spurious runs of experiment data that paint a misleading picture of what’s actually happening with your visitors and users. Sometimes referred to as false positives or type I errors, these are misleading signals from your experiment that won’t translate into true improvements over time.

Statistical errors make us grumpy, which is why we set a high statistical significance level for our experiments.
- Statistical Power: Sometimes expressed as (1 – type II error), this is the probability that an experimenter will detect a difference when it exists. It is also the probability of correctly rejecting a null hypothesis. In Optimizely’s Stats Engine, all experiments are adequately powered.
- Statistical Significance Level: The threshold of p-values an experimenter will accept. In the case where the p-value threshold is ≤ .05, statistical significance is displayed as 95%. This threshold describes the level of error an experimenter is comfortable with in a given experiment.
- Type I Error: Occurs when a conclusive result (winner or loser) is declared, and the test is actually inconclusive. This is commonly termed a “false positive.” Where “positive” is more precisely described as conclusive (can be either a winner or loser.) Hypothesis tests that calculate statistical significance are usually doing so to control these type 1 errors in experiments they run.
- Type II Error: Occurs when no conclusive result (winner or loser) is declared, failing to discover a conclusive difference between a control and variation when there was one. This is also termed a “false negative.”



