Hvordan ta statistisk forsvarlige beslutninger ved hjelp av konfidensintervaller

Som eksperimentator kan presset om å ta en beslutning etter at du har kjørt en A/B-test føre til noen ganske sprø tolkninger av ikke-signifikante eksperimentresultater. For hva betyr det egentlig at noe "trender i retning av statistisk signifikans" (en frase som faktisk ble sagt med selvtillit under en nylig eksperimentgjennomgang hos Optimizely)?

I dette innlegget skal jeg snakke om hvordan du kan bruke konfidensintervaller til å redusere risikoen ved beslutninger basert på ikke-signifikante resultater fra A/B-tester uten at det går på bekostning av din intellektuelle integritet.

Rimelige, men feilaktige påstander hørt på Optimizelys eksperimentgjennomgang

Mitt favorittmøte hos Optimizely er vår ukentlige Experiment Review. Det er et sted der folk kommer sammen for å finpusse ideer til produkteksperimenter og dele resultatene fra tidligere eksperimenter. Det er et flott sted å gi og motta tilbakemeldinger, og jeg ser frem til det hver uke.

Men i likhet med mange andre eksperimentatorer har jeg vært i den lite misunnelsesverdige situasjonen at jeg har presentert et eksperiment der ingen av måleparameterne nådde statistisk signifikans. I det øyeblikket kan presset for å få noe av verdi ut av eksperimentet være ekstremt høyt. For å komme til dette punktet måtte ideen din slå ut utallige andre fantastiske ideer for å komme øverst i backloggen. En ingeniør brukte verdifulle sykluser på å kode den. Den kjørte i flere uker. Og nå forventer teamet at du tar en datadrevet beslutning om retningen på produktet. 😬

Det fryktede "havet av grått" slår til igjen!

Å se den mentale gymnastikken eksperimentatorene går gjennom i denne situasjonen, er en av de virkelige gledene ved Experiment Review. Her er noen av de rimelig klingende, men til syvende og sist feilaktige tolkningene av ikke-statisk signifikante resultater jeg har hørt:

• "Variasjon A gjør det bedre enn kontrollgruppen i retning"
• "Variasjon A går i retning av en gevinst"
• "Variasjon A har den høyeste signifikansen av alle variasjoner, så det er et godt tegn"
• "Hvis du holdt en pistol mot hodet mitt, ville jeg nok valgt variant A."

Vi vet alle at det intellektuelt ærlige ville være å fokusere energien på å utforme neste iterasjon av testen, som har større sannsynlighet for å oppnå signifikans. Når man jobber med p-verdier, bør statistikken være svart-hvitt: Enten viser resultatene en statistisk signifikant effekt, eller så gjør de det ikke. Eller for å gi det en mer poetisk formulering:

Når jeg snakker om "retningsbestemte resultater", trøster jeg meg med at jeg ikke er alene om det. Faktisk har Probable Error (Matthew Hankins' humoristiske statistikkblogg) samlet en liste over kreative uttrykk for "ikke-signifikante resultater" i fagfellevurderte akademiske tidsskrifter. Noen av mine favoritter inkluderer:

• "En ikke-signifikant trend mot signifikans"
• "På randen av signifikans"
• "Ikke signifikant i ordets snevre forstand"
• "Nærmer seg, men oppnår ikke et vanlig nivå av statistisk signifikans" 🤔

Så hvis selv akademikere er tilbøyelige til å bruke denne typen feilslått logikk, hva skal vi vanlige eksperimentdødelige gjøre når vi står overfor ikke-signifikante resultater?

Konfidensintervallet kommer inn

Konfidensintervallene uttrykker en rekke mulige forbedringsverdier for målingene dine. For beregninger som ikke har oppnådd signifikans, vil dette intervallet være ganske stort og inkludere 0 (dvs. at det er en sjanse for at nullhypotesen er sann). Den gode nyheten er at dette verdiområdet gir deg en idé om øvre og nedre grense for den sanne forbedringen du ville sett hvis testen din var mer effektiv. På resultatsiden i Optimizely vil den "sanne" forbedringen for en beregning med en signifikansgrense på 90 % ha 90 % sjanse for å befinne seg innenfor konfidensintervallet.

Dermed kan du si ting som "Variasjon A's konverteringsfrekvens er sannsynligvis ikke X % dårligere enn baseline-konverteringsfrekvensen". Det kan være nok til å ta en beslutning hvis målet ditt rett og slett er å ikke skade ytelsen ved å gjøre en endring, og det høres mye bedre ut enn å kalle det "en retningsbestemt vinner".

Jeg har selv opplevd denne situasjonen. Ta for eksempel en test jeg kjørte på Optimizely Experiment Overview-siden. Hypotesen: Ved å vise antall besøkende for hvert eksperiment på denne siden vil det bli enklere for brukerne å finne relevante data uten å måtte klikke seg inn på resultatsiden for hver test:

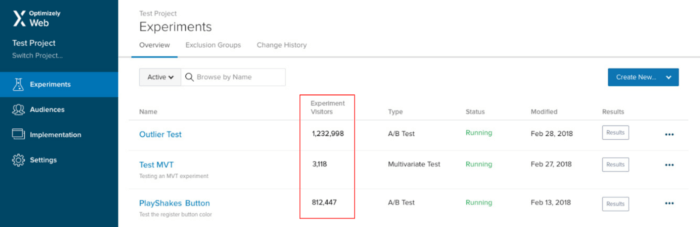
Ideen er enkel, validert av tilbakemeldinger fra kunder og gir intuitiv mening. Problemet er bare: Hvordan skal man ta en datadrevet beslutning om å lansere det? Noen i teamet trodde at brukere som ble eksponert for behandlingen, ville se færre resultatsider, mens andre mente at det kunne øke antall visninger av resultatsidene (ettersom brukere som ellers ikke ville sett på resultatene, ble nysgjerrige). Og hvis noen brukere økte forbruket av resultatsiden, mens andre reduserte forbruket, hvordan skulle vi da kunne se på resultatene fra testen hva som kunne være flatt?

Til slutt bestemte vi oss for at den eneste grunnen til at vi ikke ville gjøre denne endringen, var hvis vi så et stort fall i forbruket av resultatsiden over hele linjen.

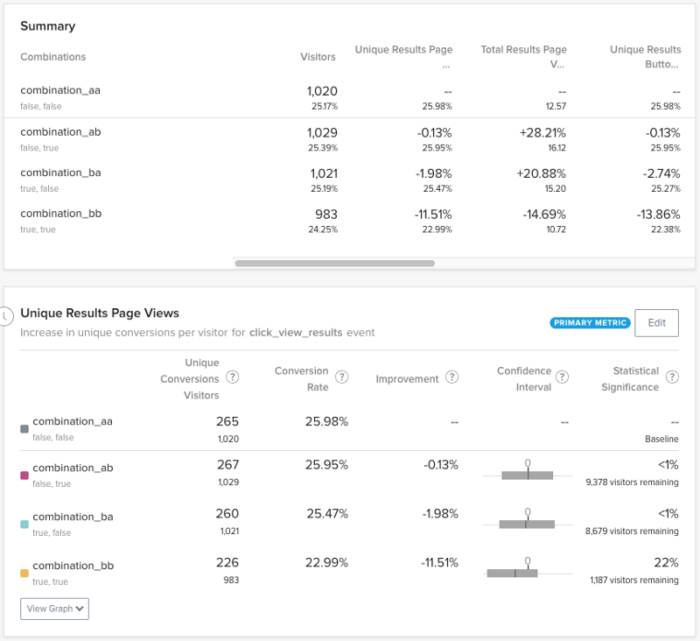
Etter å ha kjørt eksperimentet i over en måned, var det på tide å analysere resultatene. Som vi hadde fryktet, hadde ikke det primære målet vårt oppnådd signifikans, og vi måtte ta en beslutning om hva vi skulle gjøre videre. Ved å undersøke konfidensintervallet for variasjonen i "Experiment Visitors" kunne vi fastsette en "nedre grense" for forbedring:

Selv om dette konfidensintervallet er ganske bredt, hjalp det oss med å forstå hvor stor risiko vi tok ved å gjøre denne endringen. Med andre ord var det verste scenarioet at denne endringen ville redusere konverteringen til resultatsiden med ca. 22 %. Gitt det faktum at det å gjøre det enklere å finne relevante resultater fra eksperimentet rimeligvis kunne redusere antallet irrelevante resultatsider, virket dette som en akseptabel avveining.

Evne til å ta en statistisk stringent beslutning med ikke-signifikante beregninger? Sjekket! Takk for konfidensintervallet!