How to Make Statistically Sound Decisions Using Confidence Intervals
As an experimenter, the pressure to make a decision after you’ve run an A/B test can lead to some pretty wacky interpretations of non-significant experiment results. After all, what does it even mean for something to be “trending in the direction of statistical significance” (a phrase actually stated confidently during a recent experiment review at

Evan Weiss

As an experimenter, the pressure to make a decision after you’ve run an A/B test can lead to some pretty wacky interpretations of non-significant experiment results. After all, what does it even mean for something to be “trending in the direction of statistical significance” (a phrase actually stated confidently during a recent experiment review at Optimizely)?
In this post, I’ll talk about how you can use confidence intervals to de-risk decisions based on non-significant A/B test results without compromising your intellectual integrity.
Reasonable sounding but fallacious statements heard at Optimizely’s Experiment Review
My favorite meeting at Optimizely is our weekly Experiment Review. It’s a place where people come together to hone product experiment ideas and share the results of past experiments. It’s a great place to give and receive feedback, and I look forward to it every week.
But I, like many experimenters, have been in the unenviable position of presenting an experiment where none of the metrics reached statistical significance. In that moment, the pressure to glean something of value from the experiment can be extremely high. To get to this point, your idea had to beat out countless other awesome ideas to rise to the top of the backlog. An engineer spent valuable cycles coding it up. It ran for weeks. And now, the team is looking to you to make a data-driven decision about the direction of the product. 😬
The dreaded “sea of grey” strikes again!
Watching the mental gymnastics experimenters go through in this situation is one of the true joys of Experiment Review. Here are some of the reasonable-sounding but ultimately fallacious interpretations of non-statically significant results I’ve heard:
- “Directionally speaking, Variation A is outperforming the control”
- “Variation A is trending in the direction of a win”
- “Variation A has the highest significance of all variations, so that’s a good sign”
- “If you held a gun to my head, I guess I’d go with Variation A”
We all know that the intellectually honest thing to do would be to focus our energy on designing the next iteration of the test, which would be more likely to reach significance. When working with p-values, stats should be black and white: either the results show a statistically significant effect or they don’t. Or to give it a more poetic phrasing:

When I find myself talking about “directional results,” I take comfort in the fact that I’m not alone. In fact, Probable Error (Matthew Hankins’ humorous stats blog) compiled a list of creative language for “non-significant results” found in peer-reviewed academic journals. Some of my favorites include:
- “A nonsignificant trend toward significance”
- “Teetering on the brink of significance”
- “Not significant in the narrow sense of the word”
- “Approaches but fails to achieve a customary level of statistical significance” 🤔
So if even career academics are prone to this sort of flawed logic, what should we mere experimentation mortals do when faced with non-significant results?
Enter the Confidence Interval
Confidence intervals express a range of possible improvement values for your metrics. For metrics which haven’t reached significance, that range will be quite large and will include 0 (i.e. there’s a chance that the null hypothesis is true). The good news is that this range of values gives you an idea of the upper and lower bounds for the true improvement that you would see if your test were more powerful. On the Optimizely results page, the “true” improvement for a metric with a significance threshold of 90% will have a 90% chance of existing within the confidence interval.
This lets you say things like “Variation A’s conversion rate is likely not X% worse than the baseline conversion rate.” It might be enough to make a decision if your goal is simply not to hurt performance by making a change, and it sounds a lot better than calling it “a directional winner.”
I’ve encountered this situation myself. Take, for example, a test I ran on the Optimizely Experiment Overview page. The hypothesis: Displaying visitor counts for each experiment on this page will make it easier for users to find relevant data without having to click into the Results page for each test:
The idea is straightforward, validated by customer feedback, and just makes intuitive sense. The trouble is: how to make a data-driven decision about rolling it out? Some on the team thought that users who were exposed to the treatment would view fewer results pages, while others thought it might increase Results page views (as users who wouldn’t otherwise view results became curious). And if some users increased consumption of the Results page while others decreased their consumption, how would we be able to tell from our test results which could be flat?
Ultimately, we decided that the only reason we wouldn’t want to make this change was if we saw a big drop in results page consumption across the board.
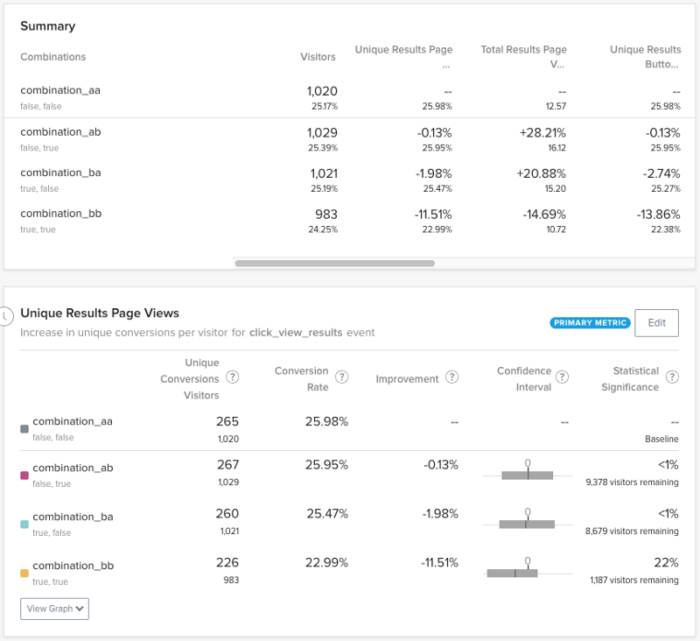
After running the experiment for over a month, it was time to analyze the results. As we had feared, our primary metric had not achieved significance, and we needed to make a decision about what to do next. By examining the confidence interval for the “Experiment Visitors” variation, we were able to establish a “lower bound” of improvement:

Even though this confidence interval is quite broad, it helped us understand the level of risk we were taking in making this change. In other words, the worst-case scenario was that making this change would decrease conversions to the results page by ~22%. Given the fact that making it easier to find relevant experiment results could reasonably decrease the number of irrelevant results pages viewed, this seemed like an acceptable tradeoff.
Ability to make a statistically rigorous decision with non-significant metrics? Check! Thanks confidence interval!
Learn more about how Optimizely Stats Engine calculates statistical significance and confidence intervals. Get the whitepaper.
